
Los diez mejores museos del segundo semestre
Los diez museos que menciono a continuación los visité en el primer semestre de 2025, pero las reseñas de mis recorridos por los mismos aparecieron a lo largo del segundo semestre en distintos portales, que se originan en México. Son museos de Etiopía, Kenia, Tanzania y Zanzíbar.
Museo Etnográfico, Adis Ababa, Etiopía. Pertenece a la Universidad de Addis Ababa (UAA). Abrió en 1955 con la intención de conservar el patrimonio nacional. El museo se aloja en el Palacio de Guenete Leul, que el rey Haile Selassie manda construir en 1930, y luego dona a la universidad. La colección tiene más de 13 0000 objetos. Incluye manuscritos religiosos y seculares, objetos ceremoniales, iconos, pinturas, túnicas bordadas en oro y plata, paraguas, cruces y libros. Y también objetos de las distintas culturas de los pueblos originarios.
Museo Nacional, Nairobi, Kenia. El museo se establece en 1919. La exhibición se organiza en las siguientes secciones: Sala introductoria; Sala numismática; Sala orígenes del hombre; Sala de mamíferos; Sala de pájaros; Sala historia de Kenia; Sala de abejas; Sala ciclos de la vida; Sala Joy Adamson; Sala Omán – Kenya; Sala arqueológica; Sala arte contemporáneo; Sala Agá Khan. La Sala orígenes del hombre ofrece un recorrido por el desarrollo de los de los homínidos de 7 000 000 a 300 000 años. Y también de la evolución del homo en sus diferentes etapas.
Galería Nacional, Nairobi, Kenia. En museo se aloja en un edificio de principios del siglo XX y abre sus puertas en 2005. Alberga la colección que formaron Joseph y Sheila Murumbi. Reunieron obras de arte, muebles, textiles, joyas, artefactos, libros y timbres de toda África. Ellos se propusieron preservar, proteger y promover la cultura africana. La exposición se organiza en nueve salas: Pasillo de entrada; Rotonda; Sala textiles de África; Sala adornos de África; Sala artefactos de África; Sala pintores; Sala – Casa Joseph Zuzarte Murumbi; Sala libros y objetos.
Casa – Museo Karen Blixen, suburbio de Karen, Nairobi, Kenia. En esta casa vivió la escritora danesa Karen Christence Blixen-Finecke (1885-1962) de 1914 a 1931. La casa es obra de principios del siglo XX de estilo europeo. Está en medio del bosque, ahora un jardín. En 1964, el gobierno danés, para honrar a la escritora compra la casa y la dona al gobierno como un “regalo” por su independencia. El lugar adquiere importancia en 1985 después de la película autobiográfica de Karen Blixen, Out of Africa, que interpreta Marly Streep y Robert Redford. Es cuando el gobierno decide hacerla museo.
Fuerte Jesús, Mombasa, Kenia. En 2011 fue declarado como Patrimonio Cultural de la Humanidad por la Unesco. Se construye entre 1593 y 1596 por orden del rey Felipe II de España, entonces también rey de Portugal. Obra del arquitecto italiano Giovanni Battista Cairatti. Es el primer fuerte de estilo europeo que se levanta en esta región. Entre 1631 y 1875 el fuerte se gana y pierde en nueve ocasiones por las naciones que disputaban el control de Mombasa. Era una posesión vital para cualquier potencia con la intención de controlar la isla y sus alrededores.
Museo Lamu, Lamu, Kenia. Está en el Centro histórico de Lamu que desde 2001 es Patrimonio Cultural de la Humanidad por la Unesco. Se aloja en una casa de finales del siglo XIX. La colección es muy rica y en las 20 salas, los objetos que se muestran representan diferentes facetas de la herencia cultural swahili e incluyen prendas de vestir, joyas, muebles, manuscritos, amuletos, instrumentos musicales, puertas y ventanas, materiales marítimos y hallazgos arqueológicos.
Fuerte Lamu, Lamu, Kenia. Está en el Centro histórico de Lamu, que desde 2001 es Patrimonio Cultural de la Humanidad por la Unesco. A principio del siglo XIX se empieza a construir el edificio, que se termina en 1821. En 1984, el edificio se entrega a los Museos Nacionales de Kenia, que lo convierten en museo a partir de 1993.
Museo Nacional, Dar es Salaam, Tanzania. El museo abre al público en 1940. En 1948 se inaugura un edificio propio y en 1963 se construye uno nuevo, el que ahora aloja la exhibición. Esta se organiza en: Sala Cuna de la Humanidad; Sala Ciudad – Estado de Shirazi; Sala etnográfica; Sala Pintura Rupestre en África; Sala Arte Contemporáneo. La Sala Cuna de la Humanidad muestra la evolución del ser humano desde los primeros Austolopthecus Africanus de 3 000 000 de años, al desarrollo de los diversos Homo desde 1 800 000 años hasta llegar al Homo Sapiens de 200 000 años.
Museo Freddie Mercury, Zanzíbar, Tanzania. El museo se abre al público en 2002. Se encuentra en el centro histórico de la ciudad, y es la casa donde el cantante Freddie Mercury (Zanzíbar, 5 de septiembre de 1946-Kensington, Inglaterra, 24 de noviembre de 1991) vivió durante sus primeros años, antes mudarse con su familia a Inglaterra en 1963. El museo alberga fotografías, objetos personales y recuerdos relacionados con Freddie Mercury y el conjunto musical Queen’s.
Museo del Comercio de Esclavos de África del Este: 1800 – 1909, Zanzíbar, Tanzania. En 2016, el museo se abrió al público en lo que fue el Hospital Santa Mónica, construido y atendido por la Iglesia Anglicana. Se conservan parte de los sótanos donde se recluía a los esclavos. En las salas se ofrece información detallada de como operó el mercado de esclavos. Zanzíbar fue el principal centro de venta de esclavos de África Oriental. Se calcula que entre los siglos XV y XIX cerca de 15 000 000 de esclavos desde aquí fueron vendidos y llevados a otros continentes.

Envolver regalos de Navidad con formas irregulares siempre es un dolor de cabeza, pero aquí tienes la fórmula para un envoltorio perfecto.
Sin embargo, para la mayoría de quienes no somos expertos en envolver regalos, lo más probable es que el resultado final sea un envoltorio caótico, un revoltijo de papel y cinta adhesiva.
Probablemente por eso envolver regalos de Navidad no suele ser una tarea que muchos disfruten.
Pero este año quizás quieras añadir una regla y una calculadora a tus materiales para envolver regalos. Es hora de aplicar el poder de las matemáticas esta Navidad.
Pensar de forma innovadora
Quizás el artículo más fácil de envolver sean las cajas cúbicas. Pero a muchos nos cuesta cortar la cantidad justa de papel para cubrir incluso esta forma tan sencilla.
A veces nos sobra mucho papel, que terminamos doblando de forma desordenada en los extremos, o nos quedamos cortos y necesitamos improvisar un trozo adicional para cubrirlo por completo.
Sin embargo, existe una fórmula ingeniosa desarrollada por Sara Santos, matemática del King’s College de Londres, que puede ayudar no solo a reducir el desperdicio de papel, sino también a que los patrones coincidan en las uniones.
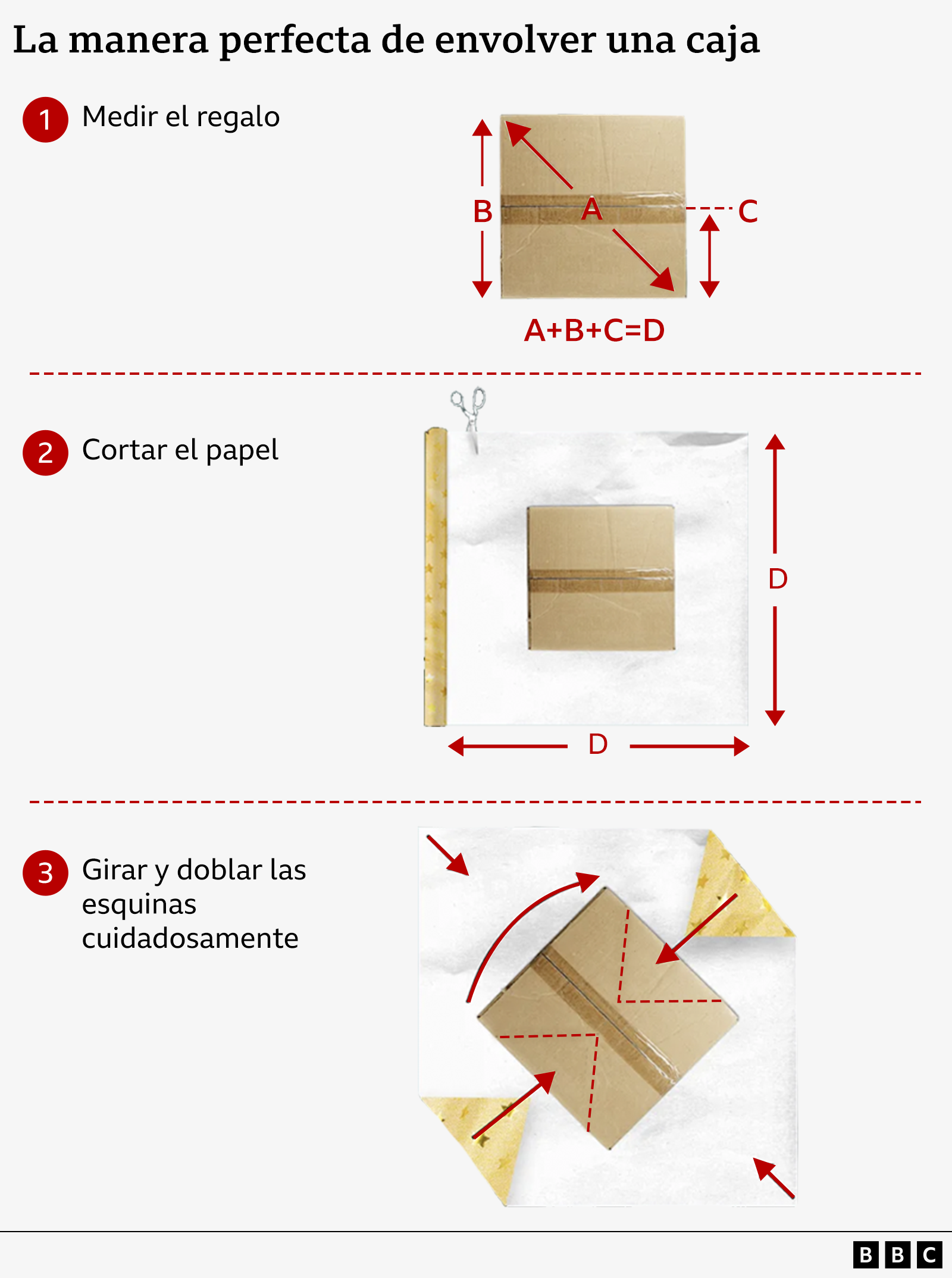
Primero, hay que medir la altura de la caja y multiplicarla por 1,5. Luego, se mide la diagonal del lado más grande de la caja, de esquina a esquina, y se suman ambas medidas. Esto proporciona las dimensiones del cuadrado de papel de regalo que se debe cortar.
Por ejemplo, si se va a envolver un cubo que mide 4,5 centímetros en diagonal y 3 cm de alto, hay que cortar un cuadrado de papel de 9 cm x 9 cm. Pero aquí viene el truco…
Cuando se coloca el regalo sobre el papel, hay que girarlo para que quede en diagonal en el centro. Luego, se dobla con cuidado las cuatro esquinas del papel hacia el centro, metiendo las solapas de cada esquina de la caja debajo de las más grandes al doblarlas.
Es importante asegurar el papel con solo tres trozos pequeños de cinta adhesiva y, si se usa papel a rayas, incluso es posible que el estampado coincida en las uniones.
Este método a veces también se puede usar para paralelepípedos.
“Sin embargo, si el papel es cuadrado, no siempre es cierto que el envoltorio diagonal sea mejor”, afirma Holly Krieger, profesora de matemáticas de la Universidad de Cambridge.
Explica, por ejemplo, que si una caja mide 2 x 4 x 8 cm, con el método diagonal se necesita un cuadrado de papel de 14 x 14 cm, pero es posible envolver el mismo regalo de forma más convencional con un cuadrado de papel de 12 cm.
El truco de la posición diagonal es más útil si se dispone de un trozo de papel cuadrado que no alcanza a cubrir un cubo de la forma tradicional.
Al colocarlo en diagonal, puede que sí se logre cubrir el regalo. De manera similar, los rectángulos de papel que no cubren completamente regalos con forma de paralelepípedo, como una caja de zapatos, se pueden adaptar si se coloca la caja en diagonal.
Solución práctica
Este método a veces también funciona para prismas triangulares.
Se mide la altura del triángulo en el extremo del empaque del prisma, se duplica y se suma la longitud total de la caja para obtener la medida perfecta de papel necesaria para cubrir sus extremos triangulares con tres capas de papel y lograr un acabado impecable.
Para envolver un tubo de caramelos u otro regalo cilíndrico con el mínimo desperdicio de papel, hay que medir el diámetro del extremo circular y multiplicarlo por por Pi (3,14…) para calcular la cantidad de papel necesaria para envolver el regalo.
Luego, se mide la longitud del tubo y suma el diámetro de un círculo para calcular la longitud mínima de papel necesaria.
De esta manera, el papel se unirá exactamente en el centro de cada extremo circular del regalo, requiriendo solo un pequeño trozo de cinta adhesiva para asegurarlo.
Sin embargo, es mejor dejar un poco de papel extra para asegurarse de que la forma quede completamente cubierta y evitar arruinar la sorpresa.

Volviendo al tema…
Si el regalo es una pelota, ¡mala suerte! Las esferas son, sin duda, la forma más difícil de envolver.
Es imposible cubrir una pelota de manera uniforme con un trozo de papel, no solo porque las propiedades del papel impiden que se doble infinitamente, sino también por el teorema de la bola peluda, explica Sophie Maclean, divulgadora de matemáticas y estudiante de doctorado en el King’s College de Londres.
Este teorema explica que es imposible peinar el pelo de una bola o esfera de forma que quede liso sin crear al menos un remolino o mechón rebelde.
“Si piensas en envolver una pelota con papel de regalo, no podrás conseguir que quede completamente lisa”, dice Maclean. “En algún punto habrá un bulto o un hueco”.
“Personalmente, me gusta ser creativa al envolver regalos, y en este caso lo aprovecharía. Ata un lazo alrededor o retuerce el papel para que parezca un caramelo o un regalo con forma de dulce”.
Si se busca la máxima eficiencia al envolver un balón de fútbol con papel, se puede probar usar un trozo de papel de aluminio con forma triangular.
Un equipo internacional de científicos estudió cómo se envuelven de forma eficiente los bombones Mozartkugel —esferas de mazapán recubiertas de praliné y bañadas en chocolate negro— con un pequeño trozo de papel de aluminio.
Observaron que minimizar el perímetro de la forma reduce el desperdicio, lo que hace que un cuadrado sea más eficiente que un rectángulo de la misma área.

Crear formas de pétalos es otra manera de cubrir una esfera de manera eficiente, aunque se necesitaría una cantidad infinita de pétalos para hacerlo con total precisión.
Sin embargo, los investigadores descubrieron que un envoltorio con forma de triángulo equilátero es aún más eficiente. “El ahorro del 0,1% del área podría resultar significativo para los millones de bombones Mozartkugel que se consumen cada año”.
Añadieron que puede haber una posible reducción del 20% en el material necesario para cubrir una forma esférica.
Probablemente todos hemos tenido dificultades para envolver regalos duros e irregulares, como una taza, que es un cilindro abierto con un asa que sobresale.
“No existe una fórmula matemática sólida que describa todas las formas posibles. Esta es una de esas situaciones en las que la experimentación es casi más útil que intentar describirlo rigurosamente de forma matemática”, dice Krieger.
Una solución podría ser combinar un regalo de forma difícil con otro para crear una figura más regular y fácil de envolver.

Máxima eficiencia sin escatimar recursos
Envolver dos regalos de tamaño similar juntos es más eficiente que envolverlos por separado, ya que requiere menos papel. Pero envolver dos regalos de formas o tamaños muy diferentes suele requerir más papel, según Krieger.
Se necesita paciencia y mucha prueba y error al agrupar formas. Incluso los matemáticos tienen dificultades.
Algunos “problemas de empaquetamiento”, como encontrar la forma más eficiente de empaquetar cuadrados idénticos dentro de un cuadrado o rectángulo más grande, se conocen como problemas “NP-difíciles”, lo que significa que son extremadamente difíciles o incluso prácticamente imposibles de resolver, aún con las computadoras más potentes.
Es un área de investigación sorprendentemente activa entre los académicos.

Ordenar esferas para que ocupen el menor espacio posible es una tarea endiabladamente difícil, así que no es de extrañar que nos cueste envolver una bolsa de pelotas de golf de forma eficiente.
Afortunadamente, los matemáticos se están ocupando del asunto, buscando la mejor manera de hacerlo.
Sin embargo, para aquellos con mentes ordenadas, la mejor solución hasta la fecha parece requerir un método de empaquetado desestructurado y bastante aleatorio, junto con algunos cálculos asombrosos.
Practicar el método de Santos puede ahorrar papel y cinta adhesiva, además de impresionar a tus familiares y amigos, pero a veces incluso los matemáticos se ven tentados a tomar atajos cuando se enfrentan a envolver regalos particularmente complicados, como pelotas.
“Quizás simplemente compre una caja”, bromea Krieger.

Haz clic aquí para leer más historias de BBC News Mundo.
Suscríbete aquí a nuestro nuevo newsletter para recibir cada viernes una selección de nuestro mejor contenido de la semana.
También puedes seguirnos en YouTube, Instagram, TikTok, X, Facebook y en nuestro nuevo canal de WhatsApp, donde encontrarás noticias de última hora y nuestro mejor contenido.
Y recuerda que puedes recibir notificaciones en nuestra app. Descarga la última versión y actívalas.
