
La historia real de *Clark Olofsson, el hombre detrás del Síndrome de Estocolmo*
Seguramente has escuchado el término “síndrome de Estocolmo” varias veces, ¿pero sabes de dónde proviene el nombre? Pues la nueva serie de Netflix Clark nos cuenta más sobre una de las personas involucradas en el Robo de Norrmalmstorg que lo originó. Te contamos más de Clark Olofsson.
Netflix sabe que el morbo nos gana y que nos encanta ver docuseries y historias basadas en crimenes reales, por eso en esta ocasión muchas personas al fin están conociendo a Clark, el hombre que logró conquistar el corazón de todo un país, aún cuando era acusado de tráfico de drogas, intento de asesinato, asalto, robo y otros crímenes.
La serie Clark de Netflix
El pasado 5 de mayo del 2022 la plataforma estrenó la serie Clark, la cual se basa en las verdades y mentiras que se revelan en la autobiografía de Clark Olofsson. La historia cuenta con seis episodios y es dirigida por Jonas Åkerlund, quien es más famoso por dirigir videos musicales de estrellas como Robbie Williams, Madonna, Lady Gaga, Rammstein, entre otros.
Clark Olofsson cobra vida gracias al actor Bill Skarsgård, a quien seguro recuerda por ser el retorcido payaso Pennywise de la saga It.
La verdadera historia de Clark Olofsson
La serie Clark presenta una versión ficticia de uno de los personajes más polémicos de la historia contemporánea de Suecia. Por eso aquí te contamos, de manera breve, cómo fue realmente el robo que le dio origen al “síndrome de Estocolmo” y qué tan involucrado estuvo este personaje.
Clark Oderth Olofsson nació en Trollhättan, Suecia y su vida se vio marcada con el engaño desde muy joven, pues luego de que su padre abandonara a su familia, y su madre ingresara a un hospital psiquiátrico, Clark y sus dos hermanas menores fueron llevadas a un hogar adoptivo.
Para escapar de esa realidad, Clark Olofsson falsificó la firma de su madre para poder embarcarse en una escuela de marineros que lo llevó de viaje por varios países.
A los 16 años, fue enviado a un reformatorio juvenil, pero a los dos años se fugó de ella junto a dos compañeros. En 1966 fue condenado a tres años de prisión por agredir a dos policías; pero logró fugarse.
Posteriormente se involucró en un crimen donde su compañero, Gunnar Norgen mató a un policía. Ahí, Clark Olofsson pasó a ser un criminal conocido en todo el país. Aunque escapó durante dos semanas, fue detenido y sentenciado a diez años de prisión.
Pero en febrero de 1969 escapó de la prisión Kumla y se fue a las Islas Canarias, luego intentó huir a Alemania donde fue detenido por usar un pasaporte falso y lo regresaron a la prisión de Kulma y sí… volvió a escaparse.
Así estuvo hasta que en 1973 fue sentenciado a seis años de prisión y posteriormente vendría el suceso que lo hizo mundialmente famoso.

El Robo de Norrmalmstorg
Era la mañana del 23 de agosto de 1973 cuando Jan-Erik “Janne” Olsson entró al banco Kreditbanken en la plaza Norrmalmstorg, en Estocolmo y debajo de su chamarra sacó una metralleta cargada que comenzó a disparar hacia el techo.
Olsson inmediatamente tomó cuatro rehenes –Gunnel Birgitta, Kristin Enmark, Elisabeth Oldgren y Sven Safstrom– y comenzó a ser exigencias a la policía: quería tres millones de coronas suecas (unos 4 millones de dólares de hoy, de acuerdo a Time), un carro para escapar y la liberación de Clark Olofsson, que en ese momento cumplía una condena.
Para sorpresa de todas las personas, la policía sueca comenzó a cumplir con sus exigencias, y no solo llegó con un Ford Mustang azul para Janne Olsson, sino también con Clark Olofsson.
Sin embargo, la policía les negó la petición de permitir que salieran llevándose a rehenes con ellos. Así fue como la pareja de criminales y las cuatro rehenes (tres mujeres y un hombre) permanecieron seis días en la bóveda del banco mientras la policía intentaba resolver esta crisis.
Pero en ese tiempo, pasó algo que solamente se explicaría por medios psicológicos: pues rehenes y criminales desarrollaron una relación de confianza como nunca antes se había visto.
Y así nació el Síndrome de Estocolmo…
El día que pasó a la historia fue el cuarto, cuando Kristin Enmark de 23 años llamó por teléfono al Primer Ministro de Suecia Olof Palme y ella le comenta que tiene más miedo de la policía que de sus propios captores.
Ella le pedía al Primer Ministro que permitiera que dos de ellas se fueran con Olsson y Olofsson como lo pedían, y de acuerdo a la BBC en la llamada ella le dijo dijo al primer ministro “Creo que está jugando con nuestras vidas. Confío plenamente en Clark y el ladrón. No nos han hecho nada. Han sido muy amables. Lo que temo es que la policía ataque y nos mate”.
Finalmente, esto terminó con la policía bombardeando el banco con gas lacrimógeno el 28 de agosto y con Janne Olsson y Clark Olofsson rindiéndose de inmediato.

Cuando la policía les pidió a las rehenes que salieran primero, las cuatro personas se negaron, pues estaban seguras de que les dispararían a sus captores. Kristin Enmark le contó a la BBC que fueron ellas mismas quienes les dijeron a Janne y Clark que salieran primero para proteger sus vidas.
Tanto BBC como History describen que en la puerta de la bóveda criminales y rehenes hicieron una pausa para despedirse entre abrazos, besos y apretones de manos.
Jane Olsson fue condenado a una pena de 10 años, mientras Clark Olofsson fue librado de toda culpa de este robo, aunque regresó a prisión para completar la condena que ya tenía.
Fue el psiquiatra y criminólogo sueco Nils Bejerot quien explicó la actitud de las rehenes de este caso como el “síndrome de Norrmalmstorg”, aunque posteriormente quedaría bautizado como el “síndrome de Estocolmo”.
¿Qué es de Clark Olofsson actualmente?
La historia de Clark no terminó después de ese famoso incidente en un banco de Estocolmo, pues su vida ha sido un constante entrar y salir de prisión.
En 1975 escapó de nuevo de la prisión de Norrköping y más tarde asaltó un banco en Copenhague, Dinamarca.
Al siguiente año hizo lo que hasta el momento era el robo más grande de Suecia, pero fue detenido. En 1979 y desde prisión, comenzó a estudiar periodismo y se graduó en 1983, el mismo año en el que fue liberado. Aunque fue arrestado un año después.
Finalmente desde 2018 vive en Suecia como un hombre libre.

Envolver regalos de Navidad con formas irregulares siempre es un dolor de cabeza, pero aquí tienes la fórmula para un envoltorio perfecto.
Sin embargo, para la mayoría de quienes no somos expertos en envolver regalos, lo más probable es que el resultado final sea un envoltorio caótico, un revoltijo de papel y cinta adhesiva.
Probablemente por eso envolver regalos de Navidad no suele ser una tarea que muchos disfruten.
Pero este año quizás quieras añadir una regla y una calculadora a tus materiales para envolver regalos. Es hora de aplicar el poder de las matemáticas esta Navidad.
Pensar de forma innovadora
Quizás el artículo más fácil de envolver sean las cajas cúbicas. Pero a muchos nos cuesta cortar la cantidad justa de papel para cubrir incluso esta forma tan sencilla.
A veces nos sobra mucho papel, que terminamos doblando de forma desordenada en los extremos, o nos quedamos cortos y necesitamos improvisar un trozo adicional para cubrirlo por completo.
Sin embargo, existe una fórmula ingeniosa desarrollada por Sara Santos, matemática del King’s College de Londres, que puede ayudar no solo a reducir el desperdicio de papel, sino también a que los patrones coincidan en las uniones.
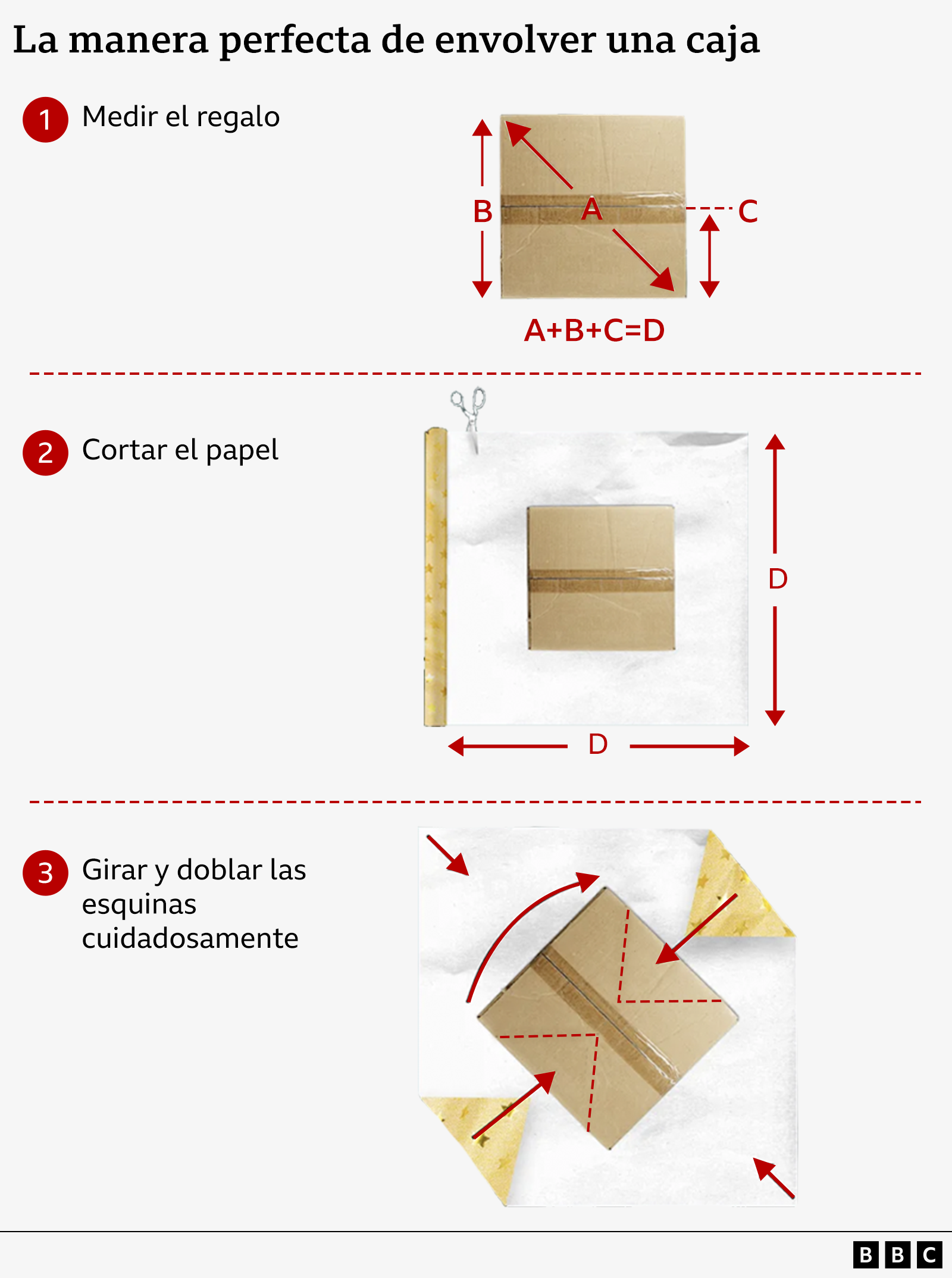
Primero, hay que medir la altura de la caja y multiplicarla por 1,5. Luego, se mide la diagonal del lado más grande de la caja, de esquina a esquina, y se suman ambas medidas. Esto proporciona las dimensiones del cuadrado de papel de regalo que se debe cortar.
Por ejemplo, si se va a envolver un cubo que mide 4,5 centímetros en diagonal y 3 cm de alto, hay que cortar un cuadrado de papel de 9 cm x 9 cm. Pero aquí viene el truco…
Cuando se coloca el regalo sobre el papel, hay que girarlo para que quede en diagonal en el centro. Luego, se dobla con cuidado las cuatro esquinas del papel hacia el centro, metiendo las solapas de cada esquina de la caja debajo de las más grandes al doblarlas.
Es importante asegurar el papel con solo tres trozos pequeños de cinta adhesiva y, si se usa papel a rayas, incluso es posible que el estampado coincida en las uniones.
Este método a veces también se puede usar para paralelepípedos.
“Sin embargo, si el papel es cuadrado, no siempre es cierto que el envoltorio diagonal sea mejor”, afirma Holly Krieger, profesora de matemáticas de la Universidad de Cambridge.
Explica, por ejemplo, que si una caja mide 2 x 4 x 8 cm, con el método diagonal se necesita un cuadrado de papel de 14 x 14 cm, pero es posible envolver el mismo regalo de forma más convencional con un cuadrado de papel de 12 cm.
El truco de la posición diagonal es más útil si se dispone de un trozo de papel cuadrado que no alcanza a cubrir un cubo de la forma tradicional.
Al colocarlo en diagonal, puede que sí se logre cubrir el regalo. De manera similar, los rectángulos de papel que no cubren completamente regalos con forma de paralelepípedo, como una caja de zapatos, se pueden adaptar si se coloca la caja en diagonal.
Solución práctica
Este método a veces también funciona para prismas triangulares.
Se mide la altura del triángulo en el extremo del empaque del prisma, se duplica y se suma la longitud total de la caja para obtener la medida perfecta de papel necesaria para cubrir sus extremos triangulares con tres capas de papel y lograr un acabado impecable.
Para envolver un tubo de caramelos u otro regalo cilíndrico con el mínimo desperdicio de papel, hay que medir el diámetro del extremo circular y multiplicarlo por por Pi (3,14…) para calcular la cantidad de papel necesaria para envolver el regalo.
Luego, se mide la longitud del tubo y suma el diámetro de un círculo para calcular la longitud mínima de papel necesaria.
De esta manera, el papel se unirá exactamente en el centro de cada extremo circular del regalo, requiriendo solo un pequeño trozo de cinta adhesiva para asegurarlo.
Sin embargo, es mejor dejar un poco de papel extra para asegurarse de que la forma quede completamente cubierta y evitar arruinar la sorpresa.

Volviendo al tema…
Si el regalo es una pelota, ¡mala suerte! Las esferas son, sin duda, la forma más difícil de envolver.
Es imposible cubrir una pelota de manera uniforme con un trozo de papel, no solo porque las propiedades del papel impiden que se doble infinitamente, sino también por el teorema de la bola peluda, explica Sophie Maclean, divulgadora de matemáticas y estudiante de doctorado en el King’s College de Londres.
Este teorema explica que es imposible peinar el pelo de una bola o esfera de forma que quede liso sin crear al menos un remolino o mechón rebelde.
“Si piensas en envolver una pelota con papel de regalo, no podrás conseguir que quede completamente lisa”, dice Maclean. “En algún punto habrá un bulto o un hueco”.
“Personalmente, me gusta ser creativa al envolver regalos, y en este caso lo aprovecharía. Ata un lazo alrededor o retuerce el papel para que parezca un caramelo o un regalo con forma de dulce”.
Si se busca la máxima eficiencia al envolver un balón de fútbol con papel, se puede probar usar un trozo de papel de aluminio con forma triangular.
Un equipo internacional de científicos estudió cómo se envuelven de forma eficiente los bombones Mozartkugel —esferas de mazapán recubiertas de praliné y bañadas en chocolate negro— con un pequeño trozo de papel de aluminio.
Observaron que minimizar el perímetro de la forma reduce el desperdicio, lo que hace que un cuadrado sea más eficiente que un rectángulo de la misma área.

Crear formas de pétalos es otra manera de cubrir una esfera de manera eficiente, aunque se necesitaría una cantidad infinita de pétalos para hacerlo con total precisión.
Sin embargo, los investigadores descubrieron que un envoltorio con forma de triángulo equilátero es aún más eficiente. “El ahorro del 0,1% del área podría resultar significativo para los millones de bombones Mozartkugel que se consumen cada año”.
Añadieron que puede haber una posible reducción del 20% en el material necesario para cubrir una forma esférica.
Probablemente todos hemos tenido dificultades para envolver regalos duros e irregulares, como una taza, que es un cilindro abierto con un asa que sobresale.
“No existe una fórmula matemática sólida que describa todas las formas posibles. Esta es una de esas situaciones en las que la experimentación es casi más útil que intentar describirlo rigurosamente de forma matemática”, dice Krieger.
Una solución podría ser combinar un regalo de forma difícil con otro para crear una figura más regular y fácil de envolver.

Máxima eficiencia sin escatimar recursos
Envolver dos regalos de tamaño similar juntos es más eficiente que envolverlos por separado, ya que requiere menos papel. Pero envolver dos regalos de formas o tamaños muy diferentes suele requerir más papel, según Krieger.
Se necesita paciencia y mucha prueba y error al agrupar formas. Incluso los matemáticos tienen dificultades.
Algunos “problemas de empaquetamiento”, como encontrar la forma más eficiente de empaquetar cuadrados idénticos dentro de un cuadrado o rectángulo más grande, se conocen como problemas “NP-difíciles”, lo que significa que son extremadamente difíciles o incluso prácticamente imposibles de resolver, aún con las computadoras más potentes.
Es un área de investigación sorprendentemente activa entre los académicos.

Ordenar esferas para que ocupen el menor espacio posible es una tarea endiabladamente difícil, así que no es de extrañar que nos cueste envolver una bolsa de pelotas de golf de forma eficiente.
Afortunadamente, los matemáticos se están ocupando del asunto, buscando la mejor manera de hacerlo.
Sin embargo, para aquellos con mentes ordenadas, la mejor solución hasta la fecha parece requerir un método de empaquetado desestructurado y bastante aleatorio, junto con algunos cálculos asombrosos.
Practicar el método de Santos puede ahorrar papel y cinta adhesiva, además de impresionar a tus familiares y amigos, pero a veces incluso los matemáticos se ven tentados a tomar atajos cuando se enfrentan a envolver regalos particularmente complicados, como pelotas.
“Quizás simplemente compre una caja”, bromea Krieger.

Haz clic aquí para leer más historias de BBC News Mundo.
Suscríbete aquí a nuestro nuevo newsletter para recibir cada viernes una selección de nuestro mejor contenido de la semana.
También puedes seguirnos en YouTube, Instagram, TikTok, X, Facebook y en nuestro nuevo canal de WhatsApp, donde encontrarás noticias de última hora y nuestro mejor contenido.
Y recuerda que puedes recibir notificaciones en nuestra app. Descarga la última versión y actívalas.



