
Así nos veríamos si hubiéramos nacido en *el espacio, la Luna o Marte*
Desde el inicio de la carrera espacial, ciencia e imaginación se han alimentado una a la otra. La película 2001: Odisea en el espacio inspiró a científicos de la NASA para diseñar naves, trajes e inteligencia artificial. A su vez, los astronautas han animado al cine a crear historias sobre el espacio como Gravity, Interstellar, The Martian y muchas otras.
¿Qué pasaría si en un futuro lográramos conquistar el espacio y vivir en él durante un largo tiempo (digamos, miles de años)? Basados en la ciencia podemos imaginar cómo las condiciones extremas de la Luna o Marte podrían transformarnos en una nueva especie.
Así que juguemos un poco y pensemos en tres posibles casos para la vida humana en el espacio: la estación internacional, que ya gravita la Tierra y va ampliándose; la Luna, que desató la carrera espacial y que podría ser una futura base; y Marte, el gigante rojo que el ser humano ya se prepara para pisar y explorar.
Checa el especial que publicamos sobre Marte: Los mexicanos que trabajan para llegar al planeta rojo

Nos toca decirte que estos escenarios son suposiciones (basadas en conocimiento científico) sobre cómo la vida humana podría evolucionar tras miles de años y cientos de generaciones.
Existen diversos factores a considerar que podrían cambiar estas predicciones o crear posibilidades que ni siquiera hemos considerado.
Aun así, muchos científicos dicen que es importante dejar volar la imaginación tomando en cuenta lo que sabemos del espacio, pues nos permite pensar en los problemas que podríamos encontrar, pero también crear posibles soluciones.
Te puede interesar: Artemisa 3, la misión que llevará a la primera mujer a la Luna
Vivir en una estación espacial
Desde que en 1961 el ruso Yuri Gagarin se convirtió en el primer hombre en el espacio, el ser humano ha hecho decenas de misiones espaciales. Esto le ha dado a los científicos ideas sobre los efectos de la falta de gravedad, la radiación, la carencia de oxígeno y otros riesgos fuera de la Tierra.
Hace un par de años, la NASA hizo un experimento sumamente interesante para analizar estos efectos.
Resulta que el astronauta estadounidense Scott Kelly tiene un hermano gemelo (y también astronauta), Mark.

Scott y Mark aceptaron participar en el experimento. Para ello, el primero se fue a vivir al espacio durante un año y el segundo permaneció en tierra.
Gracias a que son gemelos, la NASA pudo contar con dos sujetos de estudio muy parecidos y así analizar a detalle cómo afecta la vida espacial al ser humano.
Basados en los resultados de ese y otros experimentos previos podemos imaginar cómo serían los seres humanos si viviéramos durante generaciones en estaciones espaciales.
Checa también: Más misiones mexicanas a Marte: ¿qué están haciendo y dónde?
Primero, existirían efectos internos o no visibles. Se ha probado que la radiación y otros factores pueden provocar cambios en la genética, el sistema inmune y el metabolismo.
Por otro lado, sin la gravedad que atrae el flujo de sangre a las piernas, las cabezas de los astronautas se llenan de fluidos que dan como resultado el síndrome de cabeza hinchada y piernas de pájaro.
Es decir, sería posible que tras años de vivir en el espacio, tuviéramos cabezas ligeramente más grandes, piernas más delgadas, y pies más pequeños.
Los fluidos en la cabeza también pueden presionar los ojos desde adentro, lo que afectaría o deterioraría nuestra visión.
Otro de los efectos de la ingravidez es que los músculos se atrofian, los huesos pierden masa, y ambos se debilitan. Esto podría hacer que los humanos del espacio se vieran más delgados y fueran menos fuertes.
Además, si se les ocurriera volver a la Tierra, les sería casi imposible moverse y puede que hasta les doliera.
Con solo un año en el espacio, Scott Kelly creció unos 5 centímetros. La falta de gravedad ejerce menos presión sobre la espina dorsal y las vértebras se van separando muy lentamente. Así, los humanos del espacio serían más altos que los de la Tierra.

Las misiones espaciales también han revelado que nuestra piel podría hacerse más delgada y delicada, además de que podríamos volvernos más pálidos. Como Marceline… aunque ella es un vampiro.

El escenario para los seres humanos que vivieran en la Luna sería muy similar, ya que el satélite tiene una gravedad muy débil, parecida a la ingravidez del espacio. Aun así, los efectos no serían tan drásticos.
Te puede interesar: La salud mental de los astronautas que viajarán a Marte importa
¿Humanos marcianos? Así nos veríamos
Scott Solomon, biólogo evolutivo de la Universidad Rice en Texas, es autor de un libro muy interesante: Futuros humanos: Dentro de la ciencia de nuestra continua evolución.
Este investigador señala que la diferencia en la gravedad (Marte tiene sólo 38% de la gravedad terrestre) podría ocasionar que nos volviéramos más delgados, pequeños y débiles.

Por otro lado, Marte también tiene una radiación superficial mucho más alta que la Tierra. ¿Recuerdas Chernobyl? Bueno, pues esta radiación podría provocar que sufriéramos más enfermedades y con más frecuencia.

Morimos o nos adaptamos
El ser humano se ganó su lugar en la Tierra por saber aplicar su inteligencia y conocimiento para sobrevivir, sin importar las condiciones.
La ingeniería genética es algo que ya existe y que se utiliza. Podría aplicarse para ayudar a que nos adaptáramos más fácilmente a las duras condiciones del planeta rojo.
Esto, sumado a la adaptación genética natural y a que la misma radiación de Marte permitiría mutaciones genéticas más rápidas, eventualmente podrían llevar a un ser humano plenamente adaptado al planeta rojo.
Estos humanos serían más altos, robustos y fuertes que nosotros, con huesos más gruesos y músculos más densos.
Además, la radiación marciana también podría provocar que nuestra piel aumente su producción de melanina -que protege contra la radiación y oscurece la piel-.
Algunos científicos, como Solomon, piensan que incluso la piel podría volverse naranja.
La gravedad más baja también provocaría que nuestras cabezas fueran ligeramente más alargadas para facilitar el parto bajo poca gravedad.

Existen otros posibles efectos físicos de la vida en Marte, como lo ha señalada Marta Flisykowska, investigadora y diseñadora miembro del Foro Espacial de Austria.
Podríamos desarrollar extrañas narices que se adapten a la radiación, las tormentas de polvo y otros factores climáticos.
https://www.instagram.com/p/BlDHzQgBBxL/?utm_source=ig_web_copy_link
Pero todo este proceso no será rápido. El surgimiento de nuevas especies puede llevar millones de años, pero quizá “solo unos pocos cientos de generaciones, tal vez cerca de 6 mil años” sean suficientes para que la vida humana en Marte lleve al desarrollo de una nueva especie, concluye Solomon.
Relacionado

Envolver regalos de Navidad con formas irregulares siempre es un dolor de cabeza, pero aquí tienes la fórmula para un envoltorio perfecto.
Sin embargo, para la mayoría de quienes no somos expertos en envolver regalos, lo más probable es que el resultado final sea un envoltorio caótico, un revoltijo de papel y cinta adhesiva.
Probablemente por eso envolver regalos de Navidad no suele ser una tarea que muchos disfruten.
Pero este año quizás quieras añadir una regla y una calculadora a tus materiales para envolver regalos. Es hora de aplicar el poder de las matemáticas esta Navidad.
Pensar de forma innovadora
Quizás el artículo más fácil de envolver sean las cajas cúbicas. Pero a muchos nos cuesta cortar la cantidad justa de papel para cubrir incluso esta forma tan sencilla.
A veces nos sobra mucho papel, que terminamos doblando de forma desordenada en los extremos, o nos quedamos cortos y necesitamos improvisar un trozo adicional para cubrirlo por completo.
Sin embargo, existe una fórmula ingeniosa desarrollada por Sara Santos, matemática del King’s College de Londres, que puede ayudar no solo a reducir el desperdicio de papel, sino también a que los patrones coincidan en las uniones.
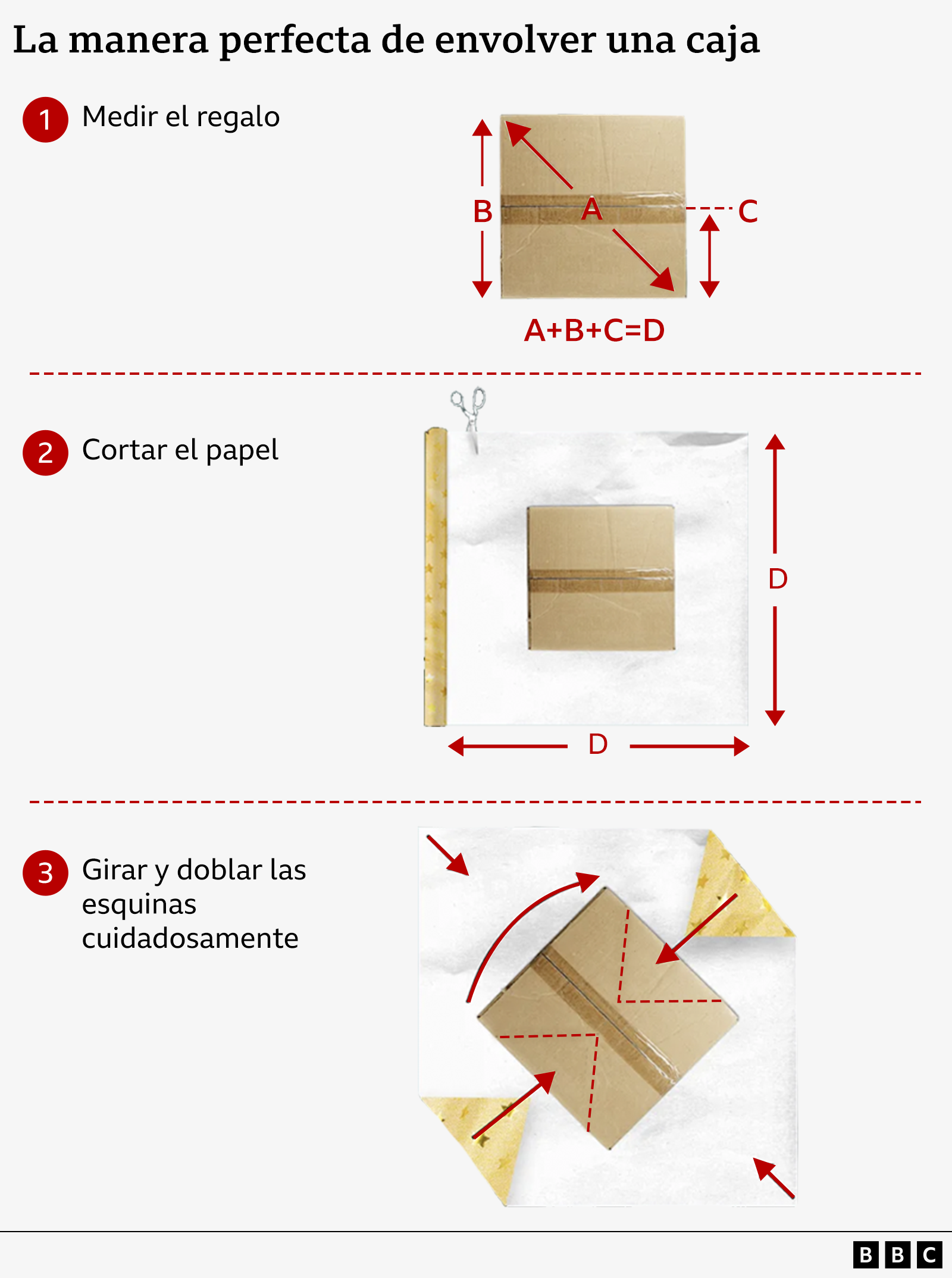
Primero, hay que medir la altura de la caja y multiplicarla por 1,5. Luego, se mide la diagonal del lado más grande de la caja, de esquina a esquina, y se suman ambas medidas. Esto proporciona las dimensiones del cuadrado de papel de regalo que se debe cortar.
Por ejemplo, si se va a envolver un cubo que mide 4,5 centímetros en diagonal y 3 cm de alto, hay que cortar un cuadrado de papel de 9 cm x 9 cm. Pero aquí viene el truco…
Cuando se coloca el regalo sobre el papel, hay que girarlo para que quede en diagonal en el centro. Luego, se dobla con cuidado las cuatro esquinas del papel hacia el centro, metiendo las solapas de cada esquina de la caja debajo de las más grandes al doblarlas.
Es importante asegurar el papel con solo tres trozos pequeños de cinta adhesiva y, si se usa papel a rayas, incluso es posible que el estampado coincida en las uniones.
Este método a veces también se puede usar para paralelepípedos.
“Sin embargo, si el papel es cuadrado, no siempre es cierto que el envoltorio diagonal sea mejor”, afirma Holly Krieger, profesora de matemáticas de la Universidad de Cambridge.
Explica, por ejemplo, que si una caja mide 2 x 4 x 8 cm, con el método diagonal se necesita un cuadrado de papel de 14 x 14 cm, pero es posible envolver el mismo regalo de forma más convencional con un cuadrado de papel de 12 cm.
El truco de la posición diagonal es más útil si se dispone de un trozo de papel cuadrado que no alcanza a cubrir un cubo de la forma tradicional.
Al colocarlo en diagonal, puede que sí se logre cubrir el regalo. De manera similar, los rectángulos de papel que no cubren completamente regalos con forma de paralelepípedo, como una caja de zapatos, se pueden adaptar si se coloca la caja en diagonal.
Solución práctica
Este método a veces también funciona para prismas triangulares.
Se mide la altura del triángulo en el extremo del empaque del prisma, se duplica y se suma la longitud total de la caja para obtener la medida perfecta de papel necesaria para cubrir sus extremos triangulares con tres capas de papel y lograr un acabado impecable.
Para envolver un tubo de caramelos u otro regalo cilíndrico con el mínimo desperdicio de papel, hay que medir el diámetro del extremo circular y multiplicarlo por por Pi (3,14…) para calcular la cantidad de papel necesaria para envolver el regalo.
Luego, se mide la longitud del tubo y suma el diámetro de un círculo para calcular la longitud mínima de papel necesaria.
De esta manera, el papel se unirá exactamente en el centro de cada extremo circular del regalo, requiriendo solo un pequeño trozo de cinta adhesiva para asegurarlo.
Sin embargo, es mejor dejar un poco de papel extra para asegurarse de que la forma quede completamente cubierta y evitar arruinar la sorpresa.

Volviendo al tema…
Si el regalo es una pelota, ¡mala suerte! Las esferas son, sin duda, la forma más difícil de envolver.
Es imposible cubrir una pelota de manera uniforme con un trozo de papel, no solo porque las propiedades del papel impiden que se doble infinitamente, sino también por el teorema de la bola peluda, explica Sophie Maclean, divulgadora de matemáticas y estudiante de doctorado en el King’s College de Londres.
Este teorema explica que es imposible peinar el pelo de una bola o esfera de forma que quede liso sin crear al menos un remolino o mechón rebelde.
“Si piensas en envolver una pelota con papel de regalo, no podrás conseguir que quede completamente lisa”, dice Maclean. “En algún punto habrá un bulto o un hueco”.
“Personalmente, me gusta ser creativa al envolver regalos, y en este caso lo aprovecharía. Ata un lazo alrededor o retuerce el papel para que parezca un caramelo o un regalo con forma de dulce”.
Si se busca la máxima eficiencia al envolver un balón de fútbol con papel, se puede probar usar un trozo de papel de aluminio con forma triangular.
Un equipo internacional de científicos estudió cómo se envuelven de forma eficiente los bombones Mozartkugel —esferas de mazapán recubiertas de praliné y bañadas en chocolate negro— con un pequeño trozo de papel de aluminio.
Observaron que minimizar el perímetro de la forma reduce el desperdicio, lo que hace que un cuadrado sea más eficiente que un rectángulo de la misma área.

Crear formas de pétalos es otra manera de cubrir una esfera de manera eficiente, aunque se necesitaría una cantidad infinita de pétalos para hacerlo con total precisión.
Sin embargo, los investigadores descubrieron que un envoltorio con forma de triángulo equilátero es aún más eficiente. “El ahorro del 0,1% del área podría resultar significativo para los millones de bombones Mozartkugel que se consumen cada año”.
Añadieron que puede haber una posible reducción del 20% en el material necesario para cubrir una forma esférica.
Probablemente todos hemos tenido dificultades para envolver regalos duros e irregulares, como una taza, que es un cilindro abierto con un asa que sobresale.
“No existe una fórmula matemática sólida que describa todas las formas posibles. Esta es una de esas situaciones en las que la experimentación es casi más útil que intentar describirlo rigurosamente de forma matemática”, dice Krieger.
Una solución podría ser combinar un regalo de forma difícil con otro para crear una figura más regular y fácil de envolver.

Máxima eficiencia sin escatimar recursos
Envolver dos regalos de tamaño similar juntos es más eficiente que envolverlos por separado, ya que requiere menos papel. Pero envolver dos regalos de formas o tamaños muy diferentes suele requerir más papel, según Krieger.
Se necesita paciencia y mucha prueba y error al agrupar formas. Incluso los matemáticos tienen dificultades.
Algunos “problemas de empaquetamiento”, como encontrar la forma más eficiente de empaquetar cuadrados idénticos dentro de un cuadrado o rectángulo más grande, se conocen como problemas “NP-difíciles”, lo que significa que son extremadamente difíciles o incluso prácticamente imposibles de resolver, aún con las computadoras más potentes.
Es un área de investigación sorprendentemente activa entre los académicos.

Ordenar esferas para que ocupen el menor espacio posible es una tarea endiabladamente difícil, así que no es de extrañar que nos cueste envolver una bolsa de pelotas de golf de forma eficiente.
Afortunadamente, los matemáticos se están ocupando del asunto, buscando la mejor manera de hacerlo.
Sin embargo, para aquellos con mentes ordenadas, la mejor solución hasta la fecha parece requerir un método de empaquetado desestructurado y bastante aleatorio, junto con algunos cálculos asombrosos.
Practicar el método de Santos puede ahorrar papel y cinta adhesiva, además de impresionar a tus familiares y amigos, pero a veces incluso los matemáticos se ven tentados a tomar atajos cuando se enfrentan a envolver regalos particularmente complicados, como pelotas.
“Quizás simplemente compre una caja”, bromea Krieger.

Haz clic aquí para leer más historias de BBC News Mundo.
Suscríbete aquí a nuestro nuevo newsletter para recibir cada viernes una selección de nuestro mejor contenido de la semana.
También puedes seguirnos en YouTube, Instagram, TikTok, X, Facebook y en nuestro nuevo canal de WhatsApp, donde encontrarás noticias de última hora y nuestro mejor contenido.
Y recuerda que puedes recibir notificaciones en nuestra app. Descarga la última versión y actívalas.




