
La masiva explosión de una estrella que será visible desde la Tierra
¡Prepárate para otro gran evento astronómico! La NASA estima que cualquier día de aquí a septiembre se podrá ver la masiva explosión de una estrella situada a tres mil años luz de la Tierra.
Este fenómeno se conoce como nova, “una explosión repentina y de corta duración procedente de una estrella compacta, no mucho más grande que la Tierra”, explica la NASA.
No confundirla con una supernova, la explosión estelar más grande que los humanos hemos podido contemplar.
¿Por qué es importante la explosión de esta estrella?
Astrónomos estiman que cada año se producen entre 20 y 50 novas (o explosiones de estrella) en nuestra galaxia. Sin embargo, casi todas pasan desapercibidas.
De hecho, las novas fueron descubiertas (y observadas) por primera vez en 1866 por el astrónomo irlandés John Birmingham. Nuevamente se pudo apreciar en 1946 y esta sería la tercera ocasión que la explosión de una estrella sea visible desde la Tierra.
Y será mejor que aproveches, porque una explosión así se podrá observar de nuevo en unos 80 años.
¿Qué ocurrirá exactamente con la nova?
El acontecimiento tendrá lugar en el sistema estelar binario T Coronae Borealis (o T CrB), perteneciente a la constelación de la Corona Boreal, que suele ser demasiado débil para ser visible a simple vista.
Sin embargo, se estima que aproximadamente cada 80 años la interacción entre estas dos estrellas desencadena una explosión nuclear que reaviva su luminosidad.

T CrB tiene normalmente una visibilidad de +10 en términos de brillo. De acuerdo con la NASA, cuando se produzca la explosión de la estrella, alcanzará una magnitud de +2, por lo que podrá observarse desde la Tierra.
Pa’que te hagas una mejor idea: la Estrella Polar tiene un nivel de brillo similar a +2 , mientras que la estrella más brillante, Sirio, tiene un nivel de -1.46 y el brillo del Sol es de -26.8.
Es por eso que parecerá que aparece una nueva estrella en el firmamento. Sin embargo, esto no es así. La estrella ha estado ahí pero gracias a la explosión se hará más visible para nosotros.
Cuándo y dónde ver la nova de 2024
La NASA estima que la nova de T CrB ocurrirá en cualquier momento de aquí a septiembre del 2024. Pero tranqui, no creas que explotará y solo tendrás un día para verla.
Cuando comience el proceso de la nova, se podrá calcular en qué momento será el de máximo brillo. La NASA asegura que será visible durante una semana a simple vista. En meses posteriores, podrás verla con binoculares.
Para ver la explosión de la estrella y cómo su brillo nos alcanza, tendrás que buscar en el cielo la constelación Corona Borealis, que únicamente es visible en el hemisferio norte.
Te interesa: Apps para ver las estrellas y jugarle al astrónomo
Es un arco pequeño semicircular cerca de Bootes (Boyero) y Hércules. Ahí es donde podrás ver esta “nueva” estrella cuando ocurra la explosión.

Mantente pendiente de la cuenta @NASAUniverse en X que dará noticias cuando empiece la explosión.
Relacionado

Envolver regalos de Navidad con formas irregulares siempre es un dolor de cabeza, pero aquí tienes la fórmula para un envoltorio perfecto.
Sin embargo, para la mayoría de quienes no somos expertos en envolver regalos, lo más probable es que el resultado final sea un envoltorio caótico, un revoltijo de papel y cinta adhesiva.
Probablemente por eso envolver regalos de Navidad no suele ser una tarea que muchos disfruten.
Pero este año quizás quieras añadir una regla y una calculadora a tus materiales para envolver regalos. Es hora de aplicar el poder de las matemáticas esta Navidad.
Pensar de forma innovadora
Quizás el artículo más fácil de envolver sean las cajas cúbicas. Pero a muchos nos cuesta cortar la cantidad justa de papel para cubrir incluso esta forma tan sencilla.
A veces nos sobra mucho papel, que terminamos doblando de forma desordenada en los extremos, o nos quedamos cortos y necesitamos improvisar un trozo adicional para cubrirlo por completo.
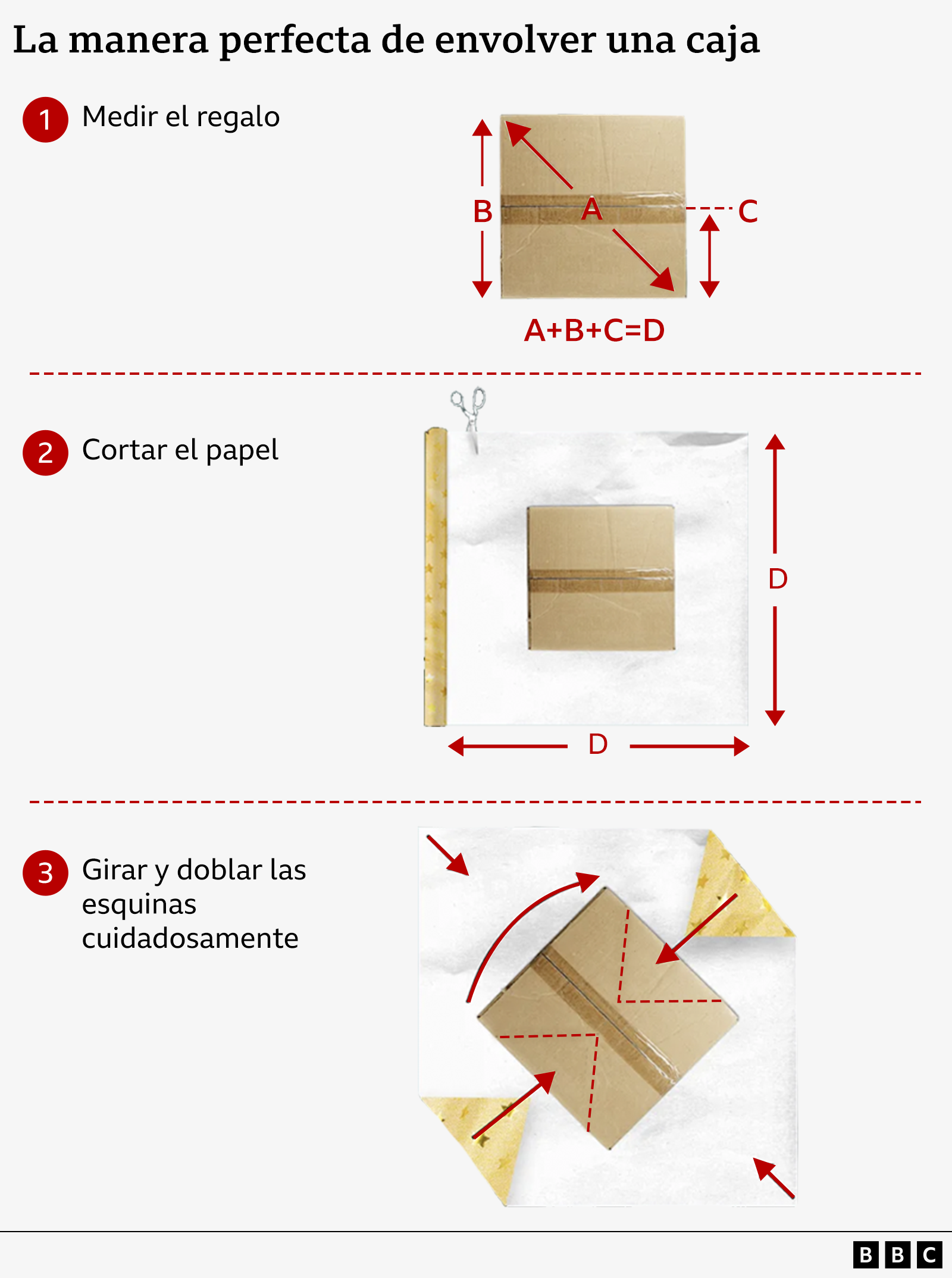
Sin embargo, existe una fórmula ingeniosa desarrollada por Sara Santos, matemática del King’s College de Londres, que puede ayudar no solo a reducir el desperdicio de papel, sino también a que los patrones coincidan en las uniones.
Primero, hay que medir la altura de la caja y multiplicarla por 1,5. Luego, se mide la diagonal del lado más grande de la caja, de esquina a esquina, y se suman ambas medidas. Esto proporciona las dimensiones del cuadrado de papel de regalo que se debe cortar.
Por ejemplo, si se va a envolver un cubo que mide 4,5 centímetros en diagonal y 3 cm de alto, hay que cortar un cuadrado de papel de 9 cm x 9 cm. Pero aquí viene el truco…
Cuando se coloca el regalo sobre el papel, hay que girarlo para que quede en diagonal en el centro. Luego, se dobla con cuidado las cuatro esquinas del papel hacia el centro, metiendo las solapas de cada esquina de la caja debajo de las más grandes al doblarlas.
Es importante asegurar el papel con solo tres trozos pequeños de cinta adhesiva y, si se usa papel a rayas, incluso es posible que el estampado coincida en las uniones.
Este método a veces también se puede usar para paralelepípedos.
“Sin embargo, si el papel es cuadrado, no siempre es cierto que el envoltorio diagonal sea mejor”, afirma Holly Krieger, profesora de matemáticas de la Universidad de Cambridge.
Explica, por ejemplo, que si una caja mide 2 x 4 x 8 cm, con el método diagonal se necesita un cuadrado de papel de 14 x 14 cm, pero es posible envolver el mismo regalo de forma más convencional con un cuadrado de papel de 12 cm.
El truco de la posición diagonal es más útil si se dispone de un trozo de papel cuadrado que no alcanza a cubrir un cubo de la forma tradicional.
Al colocarlo en diagonal, puede que sí se logre cubrir el regalo. De manera similar, los rectángulos de papel que no cubren completamente regalos con forma de paralelepípedo, como una caja de zapatos, se pueden adaptar si se coloca la caja en diagonal.
Solución práctica
Este método a veces también funciona para prismas triangulares.
Se mide la altura del triángulo en el extremo del empaque del prisma, se duplica y se suma la longitud total de la caja para obtener la medida perfecta de papel necesaria para cubrir sus extremos triangulares con tres capas de papel y lograr un acabado impecable.
Para envolver un tubo de caramelos u otro regalo cilíndrico con el mínimo desperdicio de papel, hay que medir el diámetro del extremo circular y multiplicarlo por por Pi (3,14…) para calcular la cantidad de papel necesaria para envolver el regalo.
Luego, se mide la longitud del tubo y suma el diámetro de un círculo para calcular la longitud mínima de papel necesaria.
De esta manera, el papel se unirá exactamente en el centro de cada extremo circular del regalo, requiriendo solo un pequeño trozo de cinta adhesiva para asegurarlo.
Sin embargo, es mejor dejar un poco de papel extra para asegurarse de que la forma quede completamente cubierta y evitar arruinar la sorpresa.

Volviendo al tema…
Si el regalo es una pelota, ¡mala suerte! Las esferas son, sin duda, la forma más difícil de envolver.
Es imposible cubrir una pelota de manera uniforme con un trozo de papel, no solo porque las propiedades del papel impiden que se doble infinitamente, sino también por el teorema de la bola peluda, explica Sophie Maclean, divulgadora de matemáticas y estudiante de doctorado en el King’s College de Londres.
Este teorema explica que es imposible peinar el pelo de una bola o esfera de forma que quede liso sin crear al menos un remolino o mechón rebelde.
“Si piensas en envolver una pelota con papel de regalo, no podrás conseguir que quede completamente lisa”, dice Maclean. “En algún punto habrá un bulto o un hueco”.
“Personalmente, me gusta ser creativa al envolver regalos, y en este caso lo aprovecharía. Ata un lazo alrededor o retuerce el papel para que parezca un caramelo o un regalo con forma de dulce”.
Si se busca la máxima eficiencia al envolver un balón de fútbol con papel, se puede probar usar un trozo de papel de aluminio con forma triangular.
Un equipo internacional de científicos estudió cómo se envuelven de forma eficiente los bombones Mozartkugel —esferas de mazapán recubiertas de praliné y bañadas en chocolate negro— con un pequeño trozo de papel de aluminio.
Observaron que minimizar el perímetro de la forma reduce el desperdicio, lo que hace que un cuadrado sea más eficiente que un rectángulo de la misma área.

Crear formas de pétalos es otra manera de cubrir una esfera de manera eficiente, aunque se necesitaría una cantidad infinita de pétalos para hacerlo con total precisión.
Sin embargo, los investigadores descubrieron que un envoltorio con forma de triángulo equilátero es aún más eficiente. “El ahorro del 0,1% del área podría resultar significativo para los millones de bombones Mozartkugel que se consumen cada año”.
Añadieron que puede haber una posible reducción del 20% en el material necesario para cubrir una forma esférica.
Probablemente todos hemos tenido dificultades para envolver regalos duros e irregulares, como una taza, que es un cilindro abierto con un asa que sobresale.
“No existe una fórmula matemática sólida que describa todas las formas posibles. Esta es una de esas situaciones en las que la experimentación es casi más útil que intentar describirlo rigurosamente de forma matemática”, dice Krieger.
Una solución podría ser combinar un regalo de forma difícil con otro para crear una figura más regular y fácil de envolver.

Máxima eficiencia sin escatimar recursos
Envolver dos regalos de tamaño similar juntos es más eficiente que envolverlos por separado, ya que requiere menos papel. Pero envolver dos regalos de formas o tamaños muy diferentes suele requerir más papel, según Krieger.
Se necesita paciencia y mucha prueba y error al agrupar formas. Incluso los matemáticos tienen dificultades.
Algunos “problemas de empaquetamiento”, como encontrar la forma más eficiente de empaquetar cuadrados idénticos dentro de un cuadrado o rectángulo más grande, se conocen como problemas “NP-difíciles”, lo que significa que son extremadamente difíciles o incluso prácticamente imposibles de resolver, aún con las computadoras más potentes.
Es un área de investigación sorprendentemente activa entre los académicos.

Ordenar esferas para que ocupen el menor espacio posible es una tarea endiabladamente difícil, así que no es de extrañar que nos cueste envolver una bolsa de pelotas de golf de forma eficiente.
Afortunadamente, los matemáticos se están ocupando del asunto, buscando la mejor manera de hacerlo.
Sin embargo, para aquellos con mentes ordenadas, la mejor solución hasta la fecha parece requerir un método de empaquetado desestructurado y bastante aleatorio, junto con algunos cálculos asombrosos.
Practicar el método de Santos puede ahorrar papel y cinta adhesiva, además de impresionar a tus familiares y amigos, pero a veces incluso los matemáticos se ven tentados a tomar atajos cuando se enfrentan a envolver regalos particularmente complicados, como pelotas.
“Quizás simplemente compre una caja”, bromea Krieger.

Haz clic aquí para leer más historias de BBC News Mundo.
Suscríbete aquí a nuestro nuevo newsletter para recibir cada viernes una selección de nuestro mejor contenido de la semana.
También puedes seguirnos en YouTube, Instagram, TikTok, X, Facebook y en nuestro nuevo canal de WhatsApp, donde encontrarás noticias de última hora y nuestro mejor contenido.
Y recuerda que puedes recibir notificaciones en nuestra app. Descarga la última versión y actívalas.




