
Georg Cantor, el matemático que descubrió que hay muchos infinitos y no todos son del mismo tamaño

En un chiste de matemáticos, un profesor le pregunta a la clase cuál es el número más grande. "Un trillón de billones", responde Jorge. "Y si es un trillón de billones y uno?", replica el profesor. "Bueno, estaba cerca", dice Jorge.
Los números no tienen fin. Dame un número y te daré uno más grande.
Durante miles de años, los matemáticos pensaron que el infinito estaba más allá de su comprensión.
Pero a comienzos del siglo XX, el matemático alemán Georg Cantor abordó el problema del infinito y nos mostró cómo seguir contando cuando los números se agotan.
Es uno de los momentos más emocionantes en la historia de las matemáticas. Se parece al momento en que contamos por primera vez. Pero en lugar de 1, 2, 3, contamos infinitos.
Cantor reveló que el infinito en sí mismo es un número. De hecho, infinitamente muchos números. Una revelación que desafió profundamente el establecimiento matemático.
"El verdadero logro de Cantor fue mostrar que hay infinitos más grandes que otros, algo sencillamente asombroso", señala Roger Penrose, profesor emérito de Matemáticas de la Universidad de Oxford, en conversación con la BBC.
"Entonces no se trata sólo de lo finito y lo infinito. Hay infinidades grandes, otras enormes, otras estupendamente enormes…".
Una separación
Por un tiempo, la ciencia y las matemáticas mantuvieron una relación muy íntima. Pero a mediados del siglo XIX, comenzaron a separarse.
El movimiento neohumanista de Wilhelm von Humboldt, que valoraba la educación por sí misma, en lugar de centrarse en objetivos utilitarios, alentó a los matemáticos en Alemania a pensar de forma más creativa, más imaginativa y de una manera más abstracta.
Y en ninguna parte esto se puso en práctica más que en Gotinga.
Fue allá donde Carl Gauss comenzó a remodelar las matemáticas, desarrollando nuevas teorías de los números, y donde Bernhard Riemann empujó a la gente al hiperespacio, explorando mundos que nunca podrían verse.
Y fue ahí donde el siguiente gigante de las matemáticas alemanas, Georg Cantor, aspiraba hacer su investigación.
Una pregunta
A Georg Cantor le gustaba hacer preguntas difíciles.
En su tesis doctoral, escribió: "En matemáticas, el arte de hacer preguntas es más valioso que resolver problemas".

Y para él, "la esencia de las matemáticas descansa por completo en la libertad"
Fue esa libertad la que provocó que Cantor se dirigiera en una dirección que potencialmente no tenía fin. Le atrajo la idea de tratar de capturar el infinito, algo que la mayoría de los matemáticos de la época creían imposible.
Pero, en opinión de Cantor, "el miedo al infinito es una forma de miopía que destruye la posibilidad de ver el infinito real, a pesar de que en su forma más elevada nos ha creado y sostenido".
Él iba a llevar las matemáticas a mundos cada vez más abstractos, que incluso los matemáticos de Gotinga encontraron desagradables.
¿Un infinito?
Hasta entonces, todos los infinitos habían sido agrupados bajo un encabezado. Pero Cantor quería saber si algunos infinitos eran más grandes que otros.
Fue la pregunta con la que batalló toda su vida. Cuando finalmente resolvió lo aparentemente imposible, estaba absolutamente convencido de su validez.

El infinito podía ser domesticado y comprendido.
Para quienes tienen los conocimientos suficientes para poderlos apreciar, los teoremas que Cantor son hermosos.
No obstante, en su época, hasta el eminente matemático Leopold Kronecker, quien lo había entrenado en la Universidad de Berlín y debería haber sido su más importante defensor, los consideró como un carbunclo matemático.
Una pelea
Aún así, Cantor no dio cabida a las dudas.
"Mi teoría se mantiene tan firme como una roca; cada flecha dirigida contra ella regresará rápidamente a su arquero", afirmó.

Kroneker insistió, implacable.
"No sé qué predomina en la teoría de Cantor, si la filosofía o la teología, pero estoy seguro de que lo que no hay ahí es matemáticas".
En cierto sentido, Kronecker tenía razón, las ideas de Cantor rozaban la filosofía y llegarían a cuestionar los fundamentos mismos de las matemáticas.
Cantor se defendió escribiéndole directamente al Ministro de Educación sobre el comportamiento de Kronecker.
"Yo sabía exactamente el efecto inmediato que esto tendría: que Kronecker se irritaría como si lo hubiera picado un escorpión, y con sus tropas de reserva provocaría tal aullido que Berlín pensaría que había sido transportado a los arenosos desiertos de África, con sus leones, tigres y hienas. ¡Parece que realmente logré ese objetivo!", escribió Cantor.
Pero sus comentarios no le ganaron simpatías en la comunidad matemática y comenzó a tener dificultades hasta para publicar sus ideas.
Un golpe de gracia
Poco después, recibió otro golpe, esta vez del influyente matemático sueco Gösta Mittag-Leffler, quien además era editor de la importante revista matemática Acta Mathematica.
"Estoy convencido de que la publicación de su nuevo trabajo perjudicará enormemente su reputación entre los matemáticos. Sé muy bien que, básicamente, a usted eso le da lo mismo. Pero si su teoría es desacreditada, pasará mucho tiempo antes de que vuelva a conseguir la atención del mundo matemático", le advirtió.

A Cantor le afectó profundamente el rechazo de un matemático al que respetaba mucho:
"De repente recibí una carta de Mittag–Leffler en la que escribió (para mi gran asombro) que, después de una seria consideración, consideró esta publicación como ‘aproximadamente 100 años antes de tiempo‘. De ser así, tendría que esperar hasta el año 1984, y eso me parece demasiado pedir", se lamentó.
Una lástima
La oposición de Mittag-leffler y Kronecker aseguró que Cantor nunca llegara a Gotinga: pasó el resto de sus días en los remansos de Halle, donde comenzó a sentirse cada vez más aislado.
"La visión [del infinito] que considero la única correcta es compartida por pocos. Aunque posiblemente yo sea el primero en la historia en tomar esta posición tan explícitamente, ¡estoy seguro de que no seré el último!".

Sufría episodios de depresión maníaca y la controversia sobre sus matemáticas solo empeoró las cosas.
Y a su batalla con el establecimiento se le sumó la muerte de su madre, hermano e hijo menor.
Eventualmente, Cantor fue admitido en el hospital psiquiátrico en Halle donde pasó gran parte de las últimas décadas de su vida.
Cómo contar el infinito
Cantor, al que le gustaban las preguntas, pensaba en los números como la respuesta a la pregunta: ¿cuántos?
Su gran idea surgió de imaginar que solo teníamos 4 números: 1,2,3 y muchos.

Imagínate que estás en un mercado. Tú tienes muchas monedas, el tendero tiene muchas naranjas.
Cantor se dio cuenta de que incluso si no podemos contar (porque el único número que tenemos más allá de 3 es "mucho"), aún podemos saber quién tiene más naranjas o monedas.
Lo que haríamos es emparejar la primera naranja con tu primera moneda, la siguiente naranja con tu segunda moneda, y así sucesivamente, hasta que…
- Tú te quedas sin monedas (el tendero tenía más naranjas)
- Él se queda sin naranjas (tú tenías más monedas)
- o ambos se quedan sin naranjas y monedas (tenían la misma cantidad).

Cantor aplicó la misma idea al concepto de infinito.
Descubrió, por ejemplo, que la infinidad de números enteros (1, 2, 3…) tiene el mismo tamaño que el infinito que consiste en números pares (2, 4, 6…).
Pero la sorpresa llegó cuando intentó emparejar números enteros con números decimales.
Esta vez encontró que siempre hay más números decimales que números enteros.
O dicho de manera más formal: la infinidad de todas las expansiones decimales infinitas de números es un tipo de infinito genuinamente más grande que la infinidad de números enteros.
Y no se detuvo.
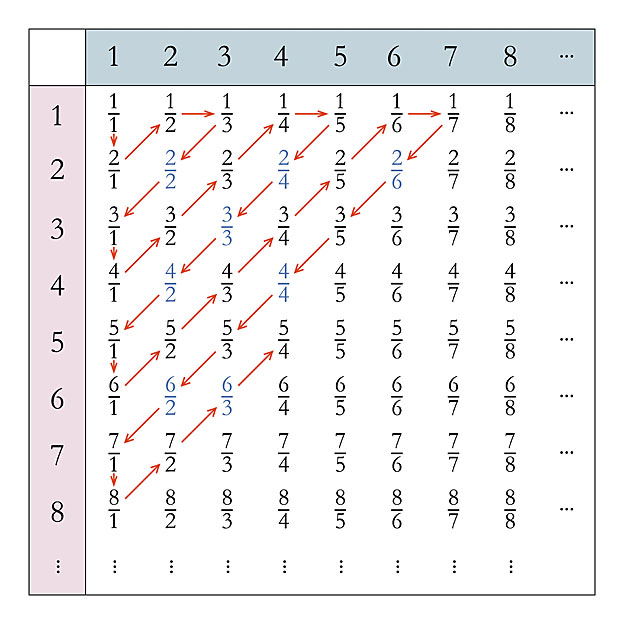
Hay más de un infinito.
De hecho, hay infinitos infinitos.
Si todo esto de desconcierta un poco, ahora entiendes lo que le pasó a los contemporáneos de Cantor, entre ellos algunas de las mejores mentes matemáticas del siglo XIX.
Una pregunta, dos respuestas
Cantor nos mostró cómo seguir contando cuando llegamos al final de nuestros números.
Mostró que puede haber infinitos conjuntos de diferentes tamaños.
Y siguió encontrando más resultados extraños, como que no existe un conjunto que sea el más grande: dado un conjunto infinito, siempre se puede hacer uno más grande.
Pero la pregunta que realmente irritó a Cantor se refería a la naturaleza del conjunto infinito de números decimales.

Sí, es más grande que el conjunto de números enteros, pero ¿podría haber un conjunto intermedio?
Un día, probaba que sí, al día siguiente, demostraba lo contrario.
¿La razón? Ambas respuestas son correctas, como se demostró algunas décadas después, una revelación por la que varias áreas de las matemáticas entraron en crisis.
El infinito mostró el límite
Las ideas de Cantor sobre los infinitos llevaron al descubrimiento de que las matemáticas mismas tienen limitaciones.
El gran lógico austríaco Kurt Godel, inspirado por el problema de Cantor, demostró en la década de 1930 que hay afirmaciones sobre números que son ciertas pero que no se pueden probar.

Roger Penrose, famoso por su comprensión de las matemáticas de los agujeros negros, recientemente ha centrado su atención en el cerebro humano.
Y cree que las matemáticas de Cantor fueron el catalizador de nuevas ideas sobre lo que hace que nuestros cerebros sean especiales (y crucialmente diferentes de las computadoras).
"El argumento que Cantor usó para mostrar que algunos infinitos son más grandes que otros infinitos muestra que el conocimiento humano no es computable", destaca Penrose.
"Es extraño, pero lo que hacemos los humanos es algo que involucra consciencia, pues el conocimiento mismo implica nuestra percepción consciente", explica.
"No tiene mucho sentido decir que entiendes algo si no estás siquiera consciente de ello", le dijo a la BBC.
El paraíso
En los albores del siglo XX, los matemáticos comenzaron a reconocer el valor las asombrosas creaciones de Cantor.
David Hilbert, que estaba emergiendo como el principal matemático de su generación en el mundo, declaró que la obra de Cantor era "el producto más asombroso del pensamiento matemático, una de las realizaciones más bellas de la actividad humana en el dominio de lo puramente inteligible".

"Nadie nos expulsará del paraíso que Cantor ha creado para nosotros", destacó Hilbert.
Como dijo Mittag-Leffler, Cantor estaba adelantado 100 años a su tiempo.
Para mediados del siglo XX, lejos de ser criticado, el genio rechazado fue acogido por las matemáticas convencionales.
Y es que las ideas de Cantor son unas de las extraordinarias de la historia.
Le han permitido a los matemáticos tocar el infinito, jugar con él y finalmente reconocer que el infinito es un número. No sólo un número sino infinitamente muchos números.
Recuerda que puedes recibir notificaciones de BBC News Mundo. Descarga la nueva versión de nuestra app y actívalas para no perderte nuestro mejor contenido.
